I was going to write about cooking today because I made yummeh foodz.
Instead, I knit on my Bayerische Sock. A lot.
Monday, December 8, 2008
Saturday, December 6, 2008
Since when is this a graph theory blog?
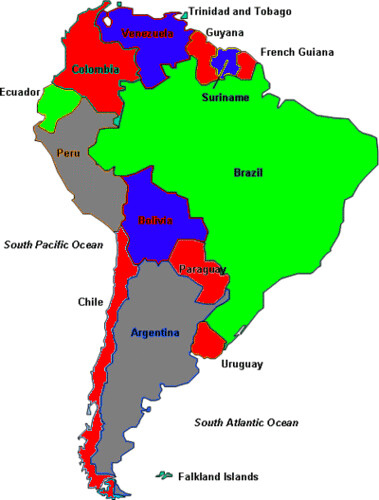
So I posted a picture of South America that I could instantly see had way more colors on it than it actually needed. How do I know this? My friends, let me tell you the way of... graph theory.
Having all those funny-shaped countries isn't convenient at all, now is it? Wouldn't it be nicer if they were easier to deal with... say, points?

Let's give Brazil some friends.
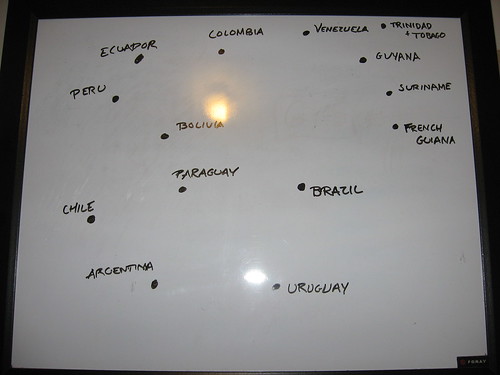
Here's where the math comes in- we're going to draw lines if there's a "symmetric relationship" between the two points. In this case, my symmetric relationship is "borders". You can't share a border with someone without having them border you, so I just draw a straight line (more about this at the end).

Now, we can see the essence of the problem. Color in the points such that no points with a line between them are the same color.
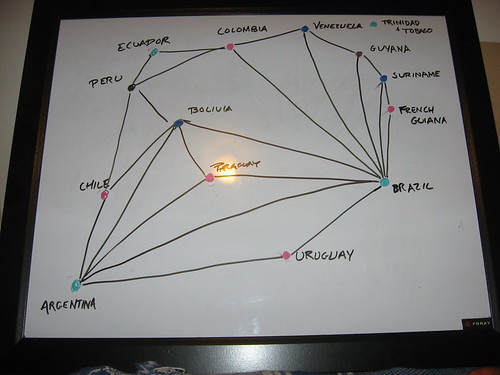
(This took me a few stops and starts- note that I forgot a few borders in the first frame, and that Argentina should be black, not green).
I ended up with this, and wasn't able to reduce any further.
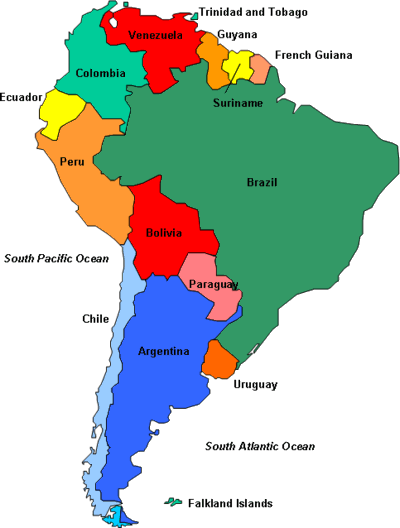
Thus, you need four colors to color this map of South America.
The Math:
This is actually a pretty famous problem - the Four Color Theorem. It's generally held that the maximum number you need to color any map is 4, although as the Wiki article says, it was proved by computer so ymmv. Or, mathematically, "the chromatic number of any planar graph is less than or equal to 4."

In this smaller case, I used a branch of mathematics called graph theory. Graph theory runs on vertices and edges: a graph is defined to be a collection of vertices V and edges E, [V,E]. You can also have a directed graph, or "digraph", of vertices V and arcs A, [V,A]. Digraphs don't make much sense in the context of this problem, but they're fun to think about and maybe I'll put up a teaser about them later.

The main concept I used to color South America is chromatic number. It's possible to force a graph to be colored with as many as n-1 colors, where n is the number of vertices; however, the chromatic number (the squiggly X is called a "xi", pronounced "khi") is the least number of colors needed. Given that there exist cycles in the graph of South America, you need at least three; in fact, before I drew in the borders between Argentina and Paraguay, the graph was three-colorable.
Having all those funny-shaped countries isn't convenient at all, now is it? Wouldn't it be nicer if they were easier to deal with... say, points?

Let's give Brazil some friends.

Here's where the math comes in- we're going to draw lines if there's a "symmetric relationship" between the two points. In this case, my symmetric relationship is "borders". You can't share a border with someone without having them border you, so I just draw a straight line (more about this at the end).

Now, we can see the essence of the problem. Color in the points such that no points with a line between them are the same color.

(This took me a few stops and starts- note that I forgot a few borders in the first frame, and that Argentina should be black, not green).
I ended up with this, and wasn't able to reduce any further.
Thus, you need four colors to color this map of South America.

The Math:
This is actually a pretty famous problem - the Four Color Theorem. It's generally held that the maximum number you need to color any map is 4, although as the Wiki article says, it was proved by computer so ymmv. Or, mathematically, "the chromatic number of any planar graph is less than or equal to 4."

In this smaller case, I used a branch of mathematics called graph theory. Graph theory runs on vertices and edges: a graph is defined to be a collection of vertices V and edges E, [V,E]. You can also have a directed graph, or "digraph", of vertices V and arcs A, [V,A]. Digraphs don't make much sense in the context of this problem, but they're fun to think about and maybe I'll put up a teaser about them later.

The main concept I used to color South America is chromatic number. It's possible to force a graph to be colored with as many as n-1 colors, where n is the number of vertices; however, the chromatic number (the squiggly X is called a "xi", pronounced "khi") is the least number of colors needed. Given that there exist cycles in the graph of South America, you need at least three; in fact, before I drew in the borders between Argentina and Paraguay, the graph was three-colorable.
They see me provin', contradictin', inductin' and making base cases, writing proofs...
Today I took the Putnam exam and it went a LOT better than I thought it would. For those of you not in the loop, the William Lowell Putnam Mathematical Competition consists of 12 questions, 10 points each, over six hours. The median and mode score are both a big fat 0. So, getting any points means you're a gangsta mathematician. I totally rocked one question- it was about n-gons, or polygons with n sides, and the look on Dr. Fink's face when I told him I solved it with derivatives was priceless.
Math: it's pretty darn cool. Here's a little brain teaser for everyone, just to show you how awesome math is...
Here's a map of South America. Look at all the colors!
Let's say I wanted to save on color printing by reducing the number of colors used in this map. How many colors do I need to use so that no one country is colored next to another?
I'll give you guys an answer and a proof tomorrow. :)
Now for actual knitting content.

This is Lisa. Lisa lives with me in our big blue house (photos forthcoming).

These are Lisa's mittens. Paton's Classic Wool Merino on my trusty size 4 DPNs, super soft and lofty, knit up really fast and pretty and for $5, and even better... she loves them! She treats them like they're made of solid gold and it truly warms my heart.
Math: it's pretty darn cool. Here's a little brain teaser for everyone, just to show you how awesome math is...
Here's a map of South America. Look at all the colors!

Let's say I wanted to save on color printing by reducing the number of colors used in this map. How many colors do I need to use so that no one country is colored next to another?
I'll give you guys an answer and a proof tomorrow. :)
Now for actual knitting content.

This is Lisa. Lisa lives with me in our big blue house (photos forthcoming).

These are Lisa's mittens. Paton's Classic Wool Merino on my trusty size 4 DPNs, super soft and lofty, knit up really fast and pretty and for $5, and even better... she loves them! She treats them like they're made of solid gold and it truly warms my heart.
Friday, December 5, 2008
Holidailies: Day 1
Evidently Michigan needs to get its act together. I woke up this morning and it's snowed. Again. I mean, I like snow. I didn't see much of it last year since Europe was freakishly warm. However, this is getting ridiculous.
So I'm done with finals and have moved on to a position as part-time physics lackey. Between now and when I go home for Christmas, I'm going to be organizing physics labs, painting stuff, organizing outings for next quarter, and probably doing more paperwork than I've ever wanted to see, ever.
Also I just found out I got Honors on my SIP! For those of you who aren't in the K Bubble, my college (Kalamazoo College) requires every senior (that's me) to do a Senior Individualized Project. This is a large and impressive-looking paper. I did a 2-unit summer SIP- the rarest kind, because mostly you get one credit per term worked on a SIP.
I can't find my camera cable, so knitting pics after I get the Putnam done tomorrow.
So I'm done with finals and have moved on to a position as part-time physics lackey. Between now and when I go home for Christmas, I'm going to be organizing physics labs, painting stuff, organizing outings for next quarter, and probably doing more paperwork than I've ever wanted to see, ever.
Also I just found out I got Honors on my SIP! For those of you who aren't in the K Bubble, my college (Kalamazoo College) requires every senior (that's me) to do a Senior Individualized Project. This is a large and impressive-looking paper. I did a 2-unit summer SIP- the rarest kind, because mostly you get one credit per term worked on a SIP.
I can't find my camera cable, so knitting pics after I get the Putnam done tomorrow.
Monday, December 1, 2008
Oh, the holidays.
I spent a very worthwhile few days at home, sleeping, eating Polish food, and getting through one of my final papers, all of my grad school applications (yay!) and rereading the book for my other final paper. Yesterday, I drove home from Detroit to Kalamazoo, in the icky yucky snow which evidently sent the fear of God into everyone on I94 and backed up for miles with no evident reason, and wrote my other paper. Two classes down, one class, one hearing, and one thesis defense to go. If I ever convince myself to get out of bed, I'm going to take my laptop over to the bagel place, nosh on a delicious bagel and drink some coffee, and spend about an hour getting my thesis defense together. Then, back to the house to snag my trumpet and go warm up for my hearing at 11:30, then to the library for more preparation with a break for a health center appointment at 1.
Because I am mildly crazy, I am going to be doing Holidailies. Watch me add the button now. Anyhow, the point is to write every day between Dec 5 and January 6. Since I normally write about my knitting, I may have to actually knit things between then too. Essentially it's Nanowrimo for those of us who are too busy in November and too ADD anyway. Hopefully it'll all be awesome 'n stuff!
Because I am mildly crazy, I am going to be doing Holidailies. Watch me add the button now. Anyhow, the point is to write every day between Dec 5 and January 6. Since I normally write about my knitting, I may have to actually knit things between then too. Essentially it's Nanowrimo for those of us who are too busy in November and too ADD anyway. Hopefully it'll all be awesome 'n stuff!
Thursday, November 27, 2008
Soooo um...
Yeah, I fail at blog postings. To make it up for you, you're going to get a photoessay: what Jax does when she's NOT at school! It'll be awesome.
Saturday, October 11, 2008
Wild Developments!
So my computer went *kerbreak* which meant that I eventually shelled out for a new one. This one, unlike the old one, has a built-in camera and Photo Booth. So, I will be taking a few pictures.
First, Bayerische Socken.

Only a little into the third leg repeat on the first sock. They're still freaking GORGEGOUS.
Second. Remember the Shapeless White Thing?

Now it is a Shapeless White Thing with a Hood:

AND has two friends:

This is a sweater. It just needs to have the ends woven in and be washed and blocked. Sooooooo yeah. That should be happening soon... exciting!
First, Bayerische Socken.

Only a little into the third leg repeat on the first sock. They're still freaking GORGEGOUS.
Second. Remember the Shapeless White Thing?

Now it is a Shapeless White Thing with a Hood:

AND has two friends:

This is a sweater. It just needs to have the ends woven in and be washed and blocked. Sooooooo yeah. That should be happening soon... exciting!
Subscribe to:
Posts (Atom)

